High Quality Compatible Triangulations for 2D Shape Morphing
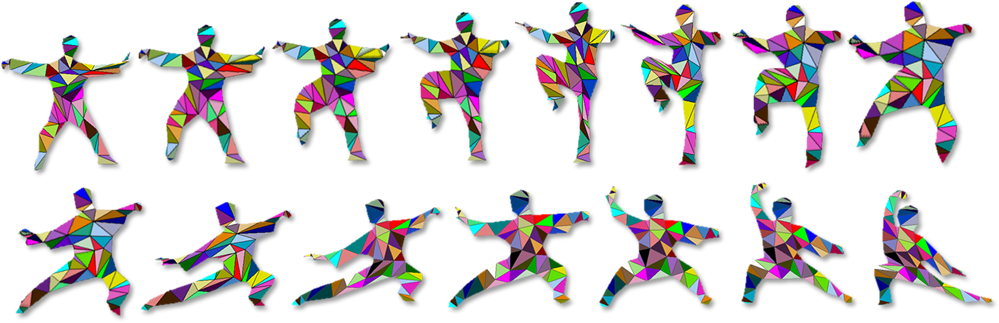
Abstract
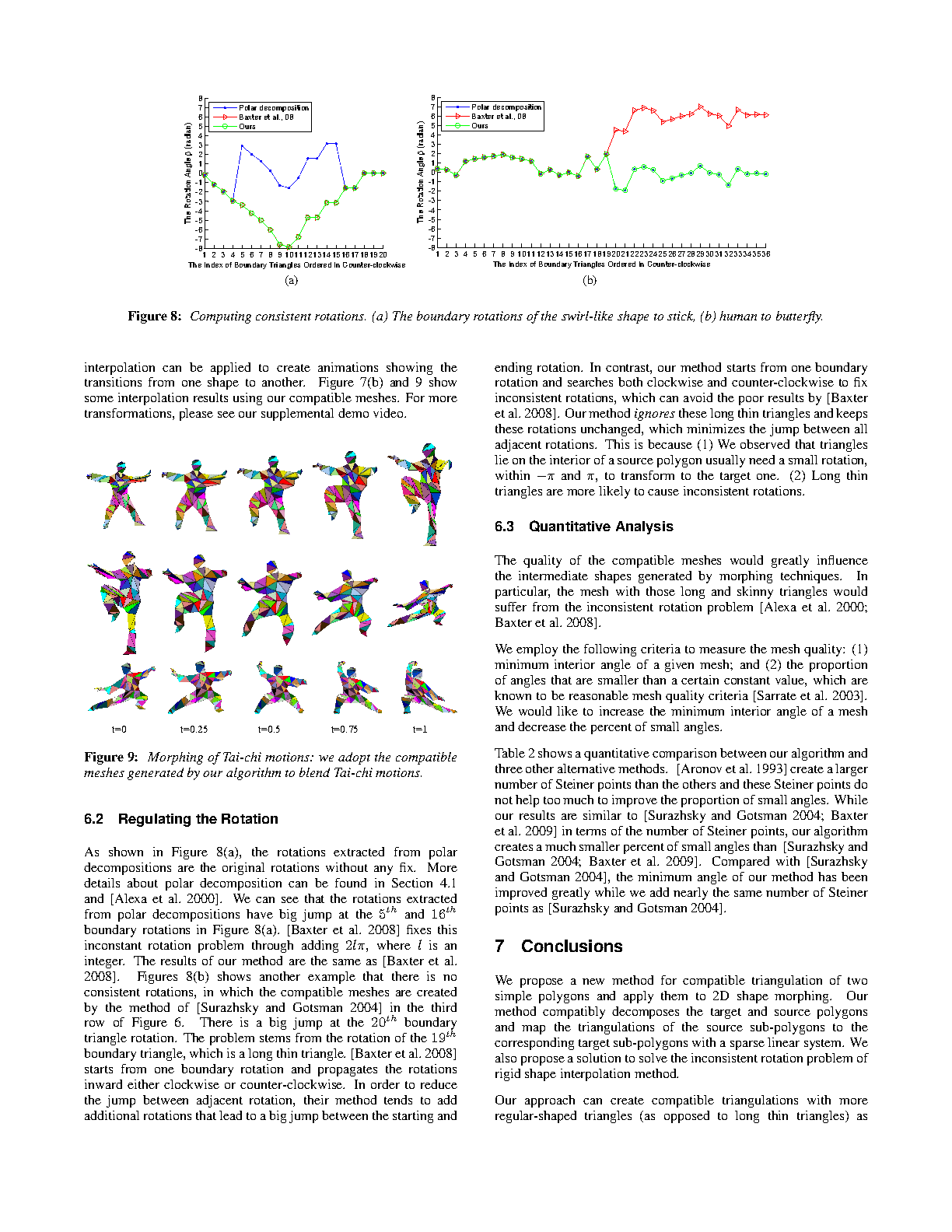
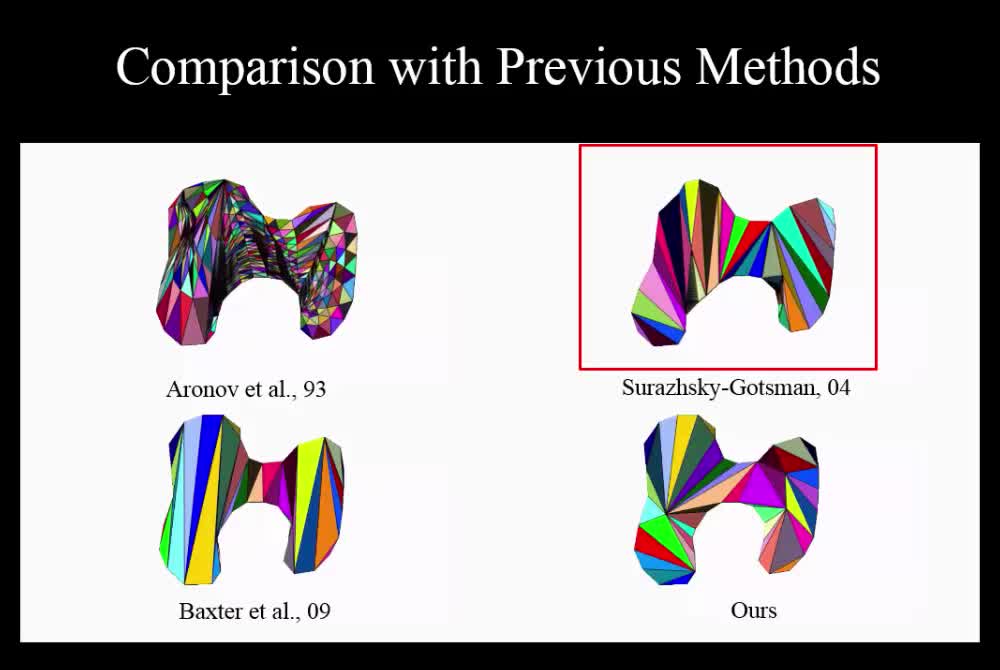
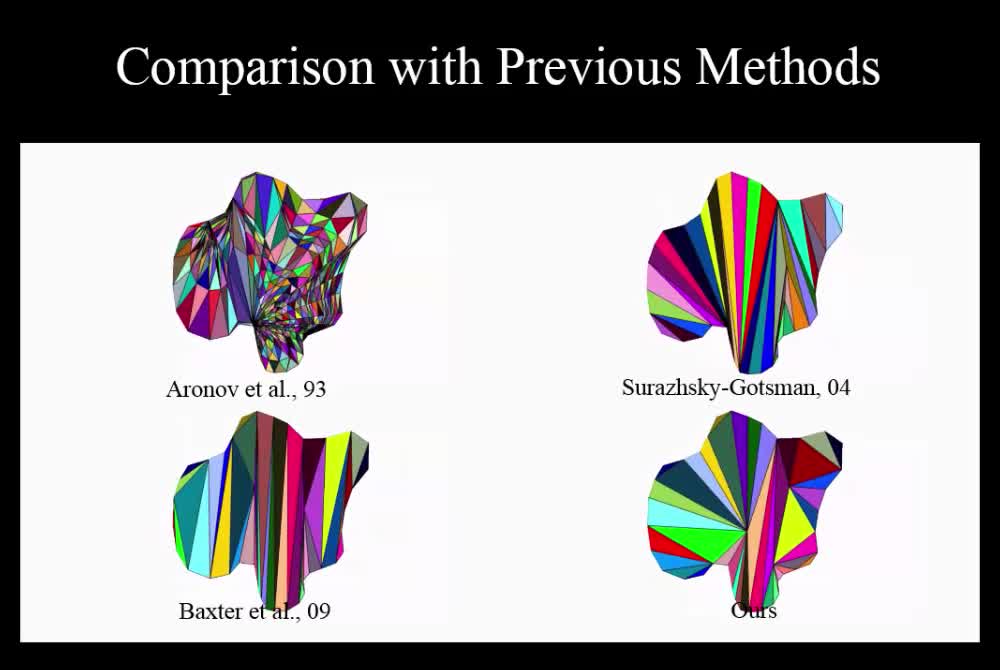
We propose a new method to compute compatible triangulations of two polygons in order to create a smooth geometric transformation between them. Compared with existing methods, our approach creates triangulations of better quality, that is, triangulations with fewer long thin triangles and Steiner points. This results in visually appealing morphing when transforming the shape from one to another. Our method consists of three stages. First, we compatibly decompose the target and source polygons into a set of sub-polygons, in which each source sub-polygon is triangulated. Second, we map the triangulation of a source sub-polygon onto the corresponding sub-polygon of the target polygon using linear transformation, thereby generating the compatible meshes between the source and the target. Third, we refine the compatible meshes, which can create better quality planar shape morphing with detailed textures. Experimental results show that our method can create compatible meshes of higher quality compared with existing methods, which facilitates smoother morphing process. The proposed algorithm is robust and computationally efficient. It can be applied to produce convincing transformations such as interactive 2D animation creation and special effects in movies.
Publication
High Quality Compatible Triangulations for 2D Shape Morphing by Pierre Plantard, Hubert P. H. Shum and Franck Multon in 2015
Proceedings of the 2015 ACM Symposium on Virtual Reality Software and Technology (VRST)
Links and Downloads
YouTube