High Quality Compatible Triangulations for Planar Shape Animation
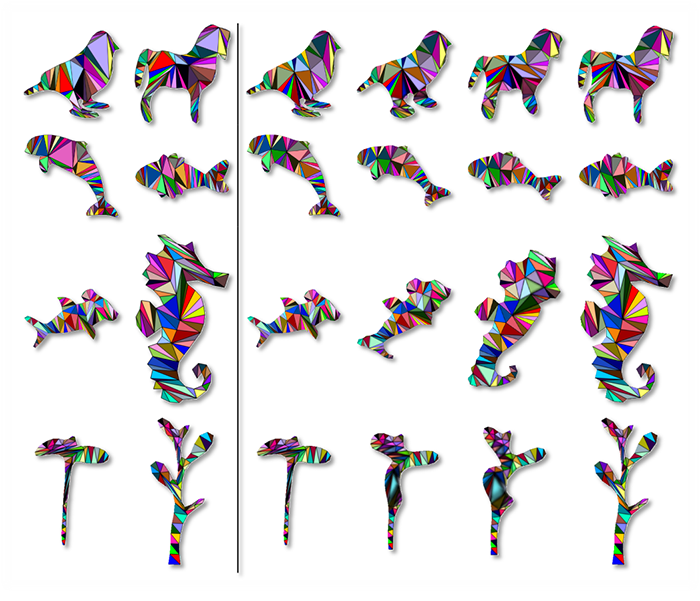
Abstract
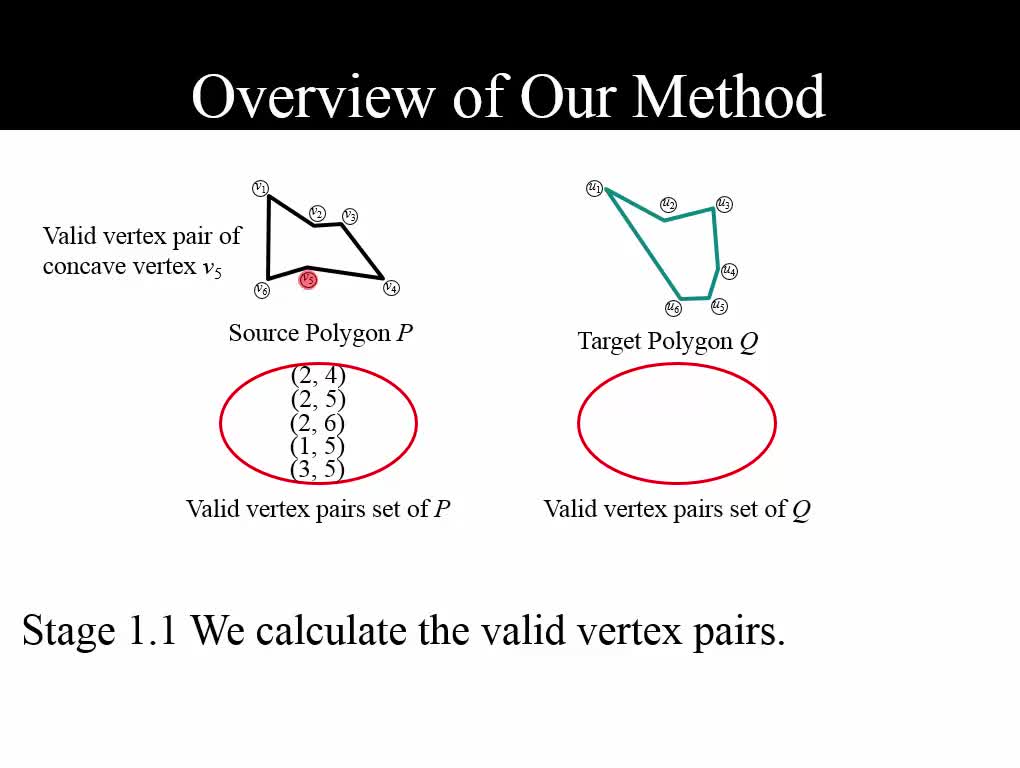
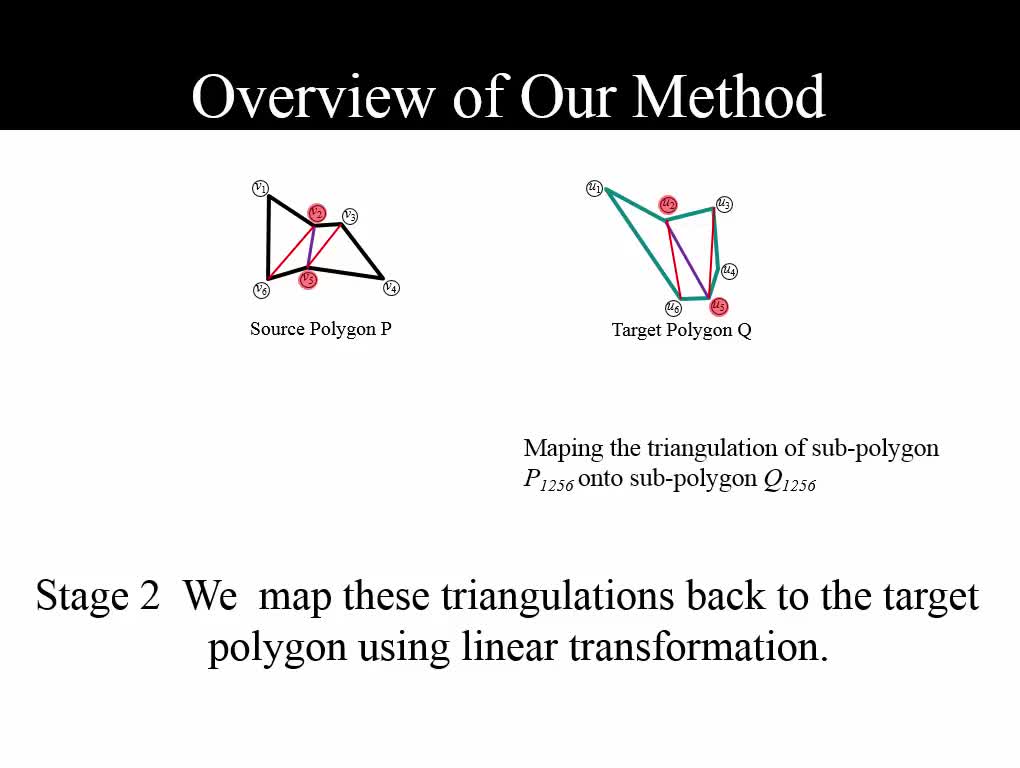
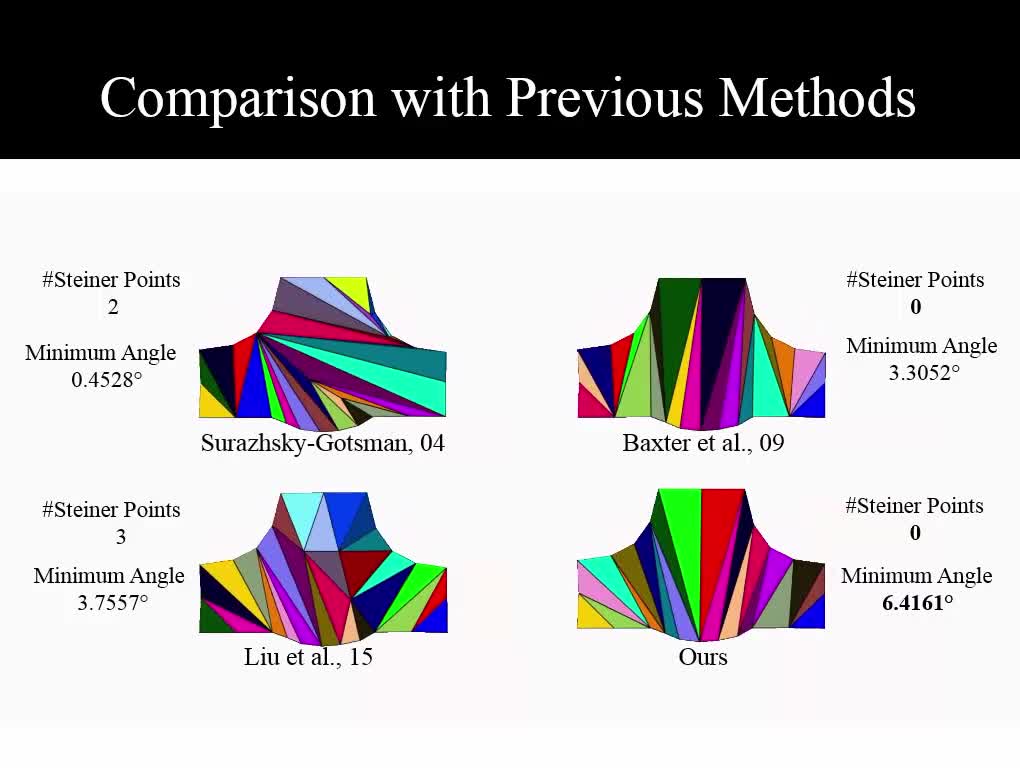
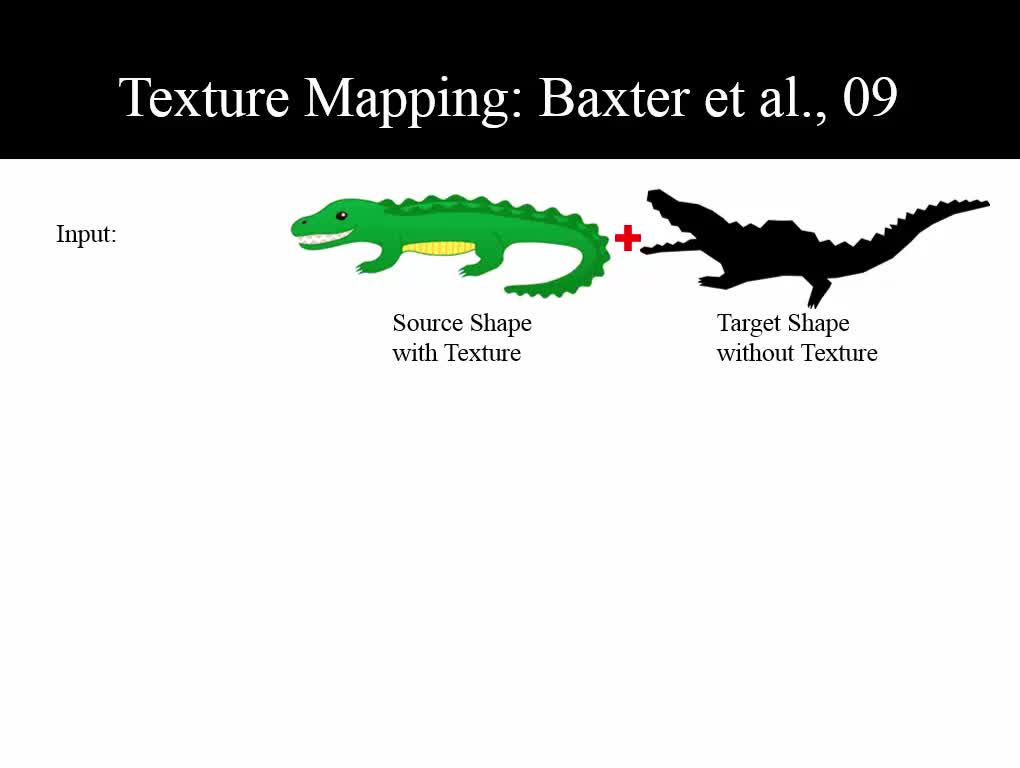
We propose a new method to compute compatible triangulations of two polygons in order to create a smooth geometric transformation between them. Compared with existing methods, our approach creates triangulations of better quality, that is, triangulations with fewer long thin triangles and Steiner points. This results in visually appealing morphing when transforming the shape from one to another. Our method consists of three stages. First, we use the common valid vertex pair to uniquely decompose the source and target polygons into pairs of sub-polygons, in which each concave sub-polygon is triangulated. Second, within each sub-polygon pair, we map the triangulation of a concave sub-polygon onto the corresponding sub-polygon using linear transformation, thereby generating compatible meshes between the source and the target. Third, we refine the compatible meshes, which can create better quality planar shape morphing with detailed textures. Experimental results show that our method can create compatible meshes of higher quality compared to existing methods with fewer long thin triangles and smaller triangle deformation values during shape morphing. These advantages enable us to create more consistent rotations for rigid shape interpolation algorithm and facilitate a smoother morphing process. The proposed algorithm is robust and computationally efficient. It can be applied to produce convincing transformations such as interactive 2D animation creation and texture mapping.
Publication
High Quality Compatible Triangulations for Planar Shape Animation by Pierre Plantard, Hubert P. H. Shum and Franck Multon in 2019
Proceedings of the 2017 ACM SIGGRAPH Asia Workshop on Data-Driven Animation Techniques (D2AT)
Links and Downloads
YouTube